markdown语法教程
此教程是对菜鸟markdown教程的精简,非常感谢菜鸟教程的分享
Markdown 是一种轻量级的标记语言
简单来说:用简单符号就能排版的写作工具,让人们回归内容本身
它通过极其简单的语法,降低了格式排版的复杂性,让你能专注于思考和创作,同时又能轻松产出格式优美、结构清晰的文档
请花几分钟,参考如下教程来快速掌握markdown语法
一、标题
标题的层次结构应该遵循逻辑顺序,不应该跳级使用。良好的标题结构就像一本书的目录
- 语法
# 一级标题
## 二级标题
### 三级标题
#### 四级标题
##### 五级标题
###### 六级标题
- 效果

二、文本
Markdown 段落没有特殊的格式,直接编写文字就好,段落的换行是使用两个以上空格加上回车
- 语法
测试1 #注意测试1后面有两个空格
测试2 #注意测试2后面有两个空格
测试3 #注意测试3后面有两个空格
- 效果
三、列表
无序列表
无序列表使用星号(*)、加号(+)或是减号(-)作为列表标记,这些标记后面要添加一个空格,然后再填写内容
- 语法
* 第一项
* 第二项
* 第三项
+ 第一项
+ 第二项
+ 第三项
- 第一项
- 第二项
- 第三项
- 效果
- 第一项
- 第二项
- 第三项
- 第一项
- 第二项
- 第三项
- 第一项
- 第二项
- 第三项
建议统一使用减号 -,因为它在视觉上更清晰
有序列表
用于展示有顺序要求的步骤或项目
有序列表使用数字并加上 . 号来表示
- 语法
1. 第一项
2. 第二项
3. 第三项
- 效果
- 第一项
- 第二项
- 第三项
任务列表
- 语法
- [ ] 未完成的任务
- [x] 已完成的任务
- [ ] 另一个未完成的任务
- 效果
- 未完成的任务
- 已完成的任务
- 另一个未完成的任务
四、引用块
引用块用于突出显示重要信息、引用他人观点或创建视觉层次
- 语法
> 区块引用
>
> markdown语法教程
>
> 学的不仅是技术更是梦想
- 效果
区块引用
markdown语法教程
学的不仅是技术更是梦想
五、代码
Markdown 提供了多种方式来展示代码,从简单的行内代码到复杂的代码块,满足不同场景下的代码展示需求
- 语法
```python
print("ok")
```
- 效果
print("ok")
六、链接
双击可打开此链接的网站
- 语法
[百度](https://baidu.com)
- 效果
七、图片
引用图片到此文件中显示
- 语法

- 效果

八、表格
- 语法
| 表头 | 表头 |
| ---- | ---- |
| 单元格 | 单元格 |
| 单元格 | 单元格 |
- 效果
| 表头 | 表头 |
|---|---|
| 单元格 | 单元格 |
| 单元格 | 单元格 |
九、分割线
Markdown 支持三种方式创建水平分割线
- 语法
使用三个连字符
---
使用三个星号
***
使用三个下划线
___
- 效果
使用三个连字符
使用三个星号
使用三个下划线
十、数学公式
在 Markdown 中,数学公式通过 LaTeX 语法来表示。
LaTeX 是一个强大的排版系统,特别适用于包含复杂数学公式的文档。
通过 Overleaf 的 Learn LaTeX in 30 minutes 等快速入门教程掌握核心概念
- 语法
$$
v = v_0 + at
$$
- 效果
十一、图表绘制
Mermaid 是最流行的 Markdown 图表工具之一,它允许你使用简单的文本语法生成各种图表
- 语法
```mermaid
graph TD
A[开始] --> B{条件判断}
B -->|Yes| C[执行操作A]
B -->|No| D[执行操作B]
C --> E[结束]
D --> E
```
- 效果
十二、实战练习
- 内容
# 高中物理教案:匀加速直线运动
## 教学目标
- 理解匀加速直线运动的基本概念
- 掌握速度、位移与加速度之间的关系
- 学会用公式解决简单的匀加速直线运动问题
## 教学重点
- 匀加速直线运动的三个基本公式
- 物理量之间的关系及其应用
## 教学过程
### 1. 导入新课
通过生活实例,如汽车起步加速,引出匀加速直线运动的概念。
### 2. 讲解公式
在匀加速直线运动中,常用的两个基本公式为:
1. **速度公式**:
$$
v = v_0 + at
$$
其中,v0 为初速度,a 为加速度,t 为时间。
2. **位移公式**:
$$
s = v_0t + \frac{1}{2}at^2
$$
其中,s 为位移。
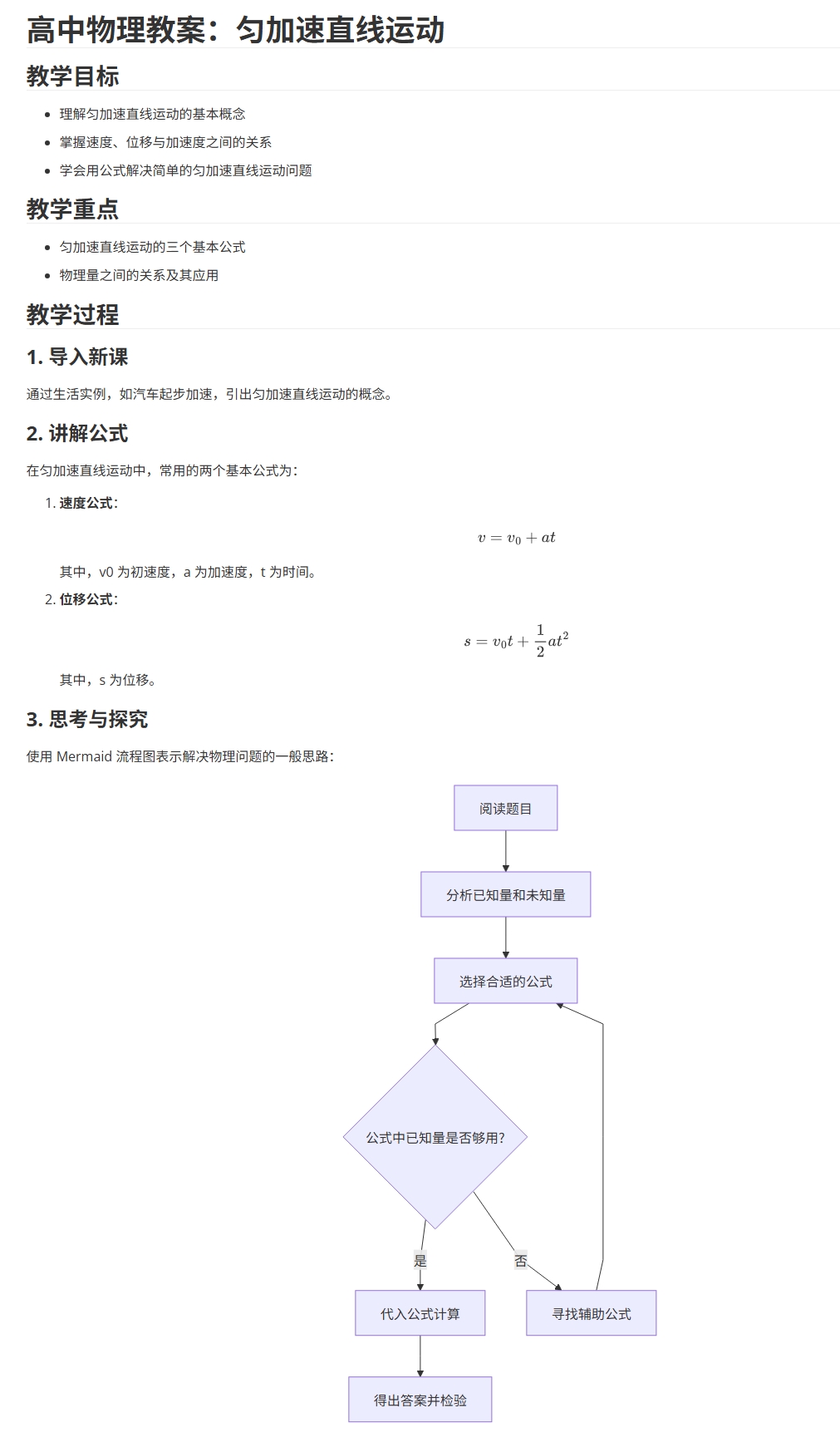
### 3. 思考与探究
使用 Mermaid 流程图表示解决物理问题的一般思路:
```mermaid
flowchart TD
A[阅读题目] --> B[分析已知量和未知量]
B --> C[选择合适的公式]
C --> D{公式中已知量是否够用?}
D -- 是 --> E[代入公式计算]
D -- 否 --> F[寻找辅助公式]
F --> C
E --> G[得出答案并检验]
- 效果